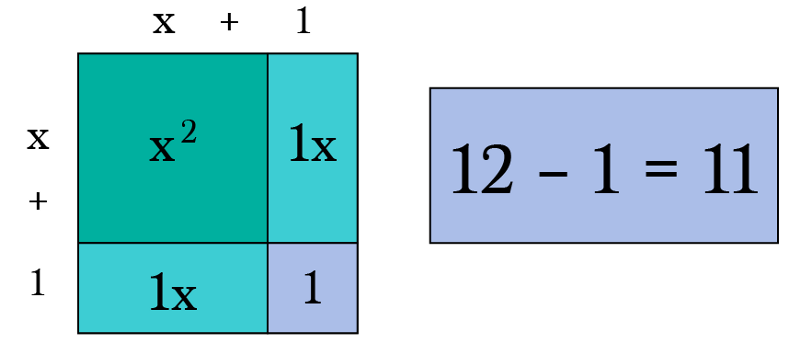
How To Complete The Square
For a quadratic polynomial.

How to complete the square. Do the same with y 2 y2 y 2 and y y y. In fact the quadratic formula that we utilize to solve quadratic equations is derived using the technique of completing the square. Now click the button solve by completing the square to get the output step 3. Magic squares have grown in popularity with the advent of mathematics based games like sudoku.
For example find the solution by completing the square for. Add a square number to both sides add the square of half the coefficient of x. I have taught completing the square 7 times twice in grad school twice in algebra 2 twice in precalculus and now once in mathematical foundations. When the integrand is a rational function with a quadratic expression in the denominator we can use the following table integrals.
B 3ar or r 1 3b a this corresponds exactly to r 1 2b a for the complete the square case then see what you have to add to both coefficients c and d to complete the cube. 2 x 2 12 x 7 0. There are 7 simple steps to completing the square. X2 x 1 x 2 x 1 to create a trinomial square on the left side of the equation find a value that is equal to the square of half of b b.
Get the answer to complete the square for x27x with the cymath math problem solver a free math equation solver and math solving app for calculus and algebra. Halve the middle term to get displaystyle frac54 this number will go in the binomial that will be squared and square it to complete the square. All this time we were rearranging the same figures that we had initially. Original equation y x2 8x 1 group first two terms.
Solving quadratic equations by completing the square steps step 1. Completing the square has a special place in my heart. That is we add t o both sides. So the completing the square equation is.
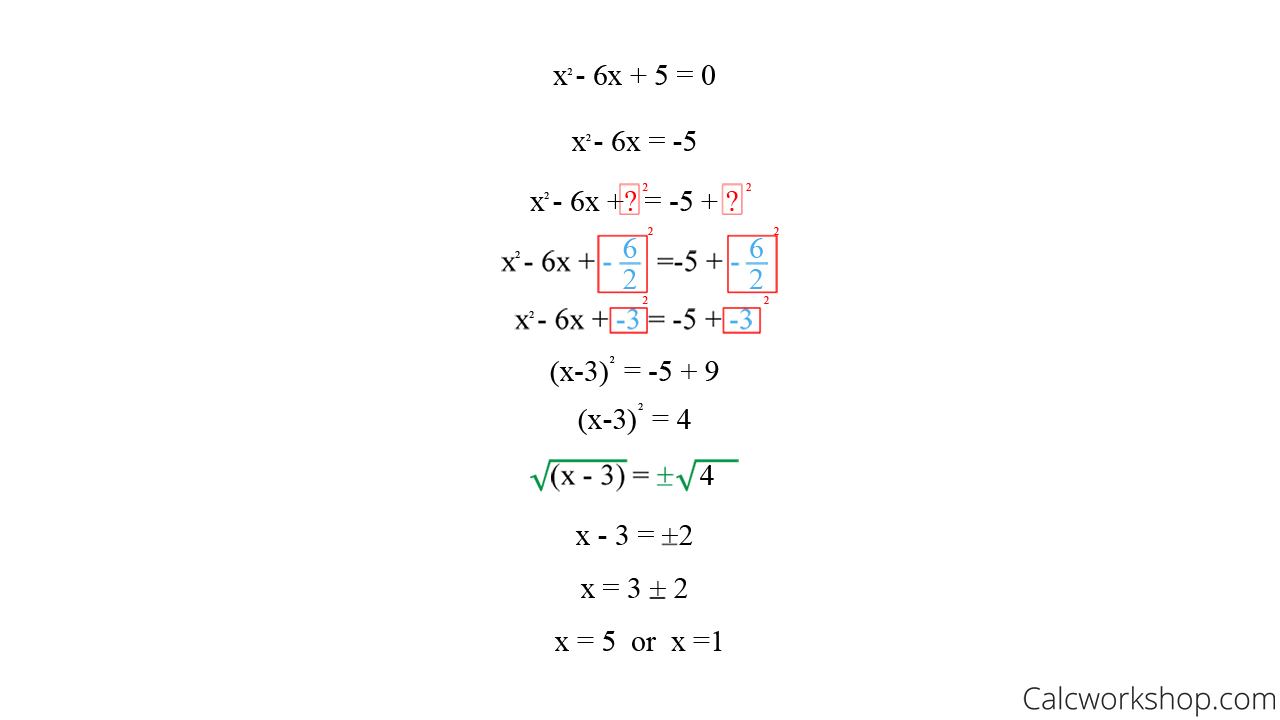
We then create a perfect square trinomial on the left by adding the square of half the coefficient of the x term to both sides. A method usually of solving quadratic equations by which a quadratic expression as x 2 4x 3 is written as the sum or difference of a perfect square and a constant x 2 4x 4 3 4 x 2 2 1 by addition and subtraction of appropriate constant terms. Factorize the x 2 x2 x 2 and the x x x term by common factor using such factor as the coefficient of x 2 x2 x 2. X7 3 or 3 by adding 7 to each side we can obtain the values for x.
Completing the square method equation. Ensure that the passed expression is quadratic with a non zero coefficient multiplying the termx 2x2 x2. In my opinion the most important usage of completing the square method is when we solve quadratic equations. The left hand side is a complete square because it results from squaring x 7.
A 1 a 2 so divide through by 2. More examples of completing the squares. If the coefficient of x 2 is 1 a 1 the above process is not required. Students learn to solve quadratic equations by completing the square.
X 7 3 or 7 3 we could write this in the briefer form x 7 3. In this case it does y 1 x2 8x 1. Add the termto each side of the equation. That is add the square of 3 which is 9.
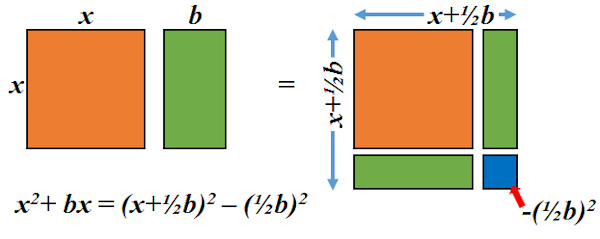
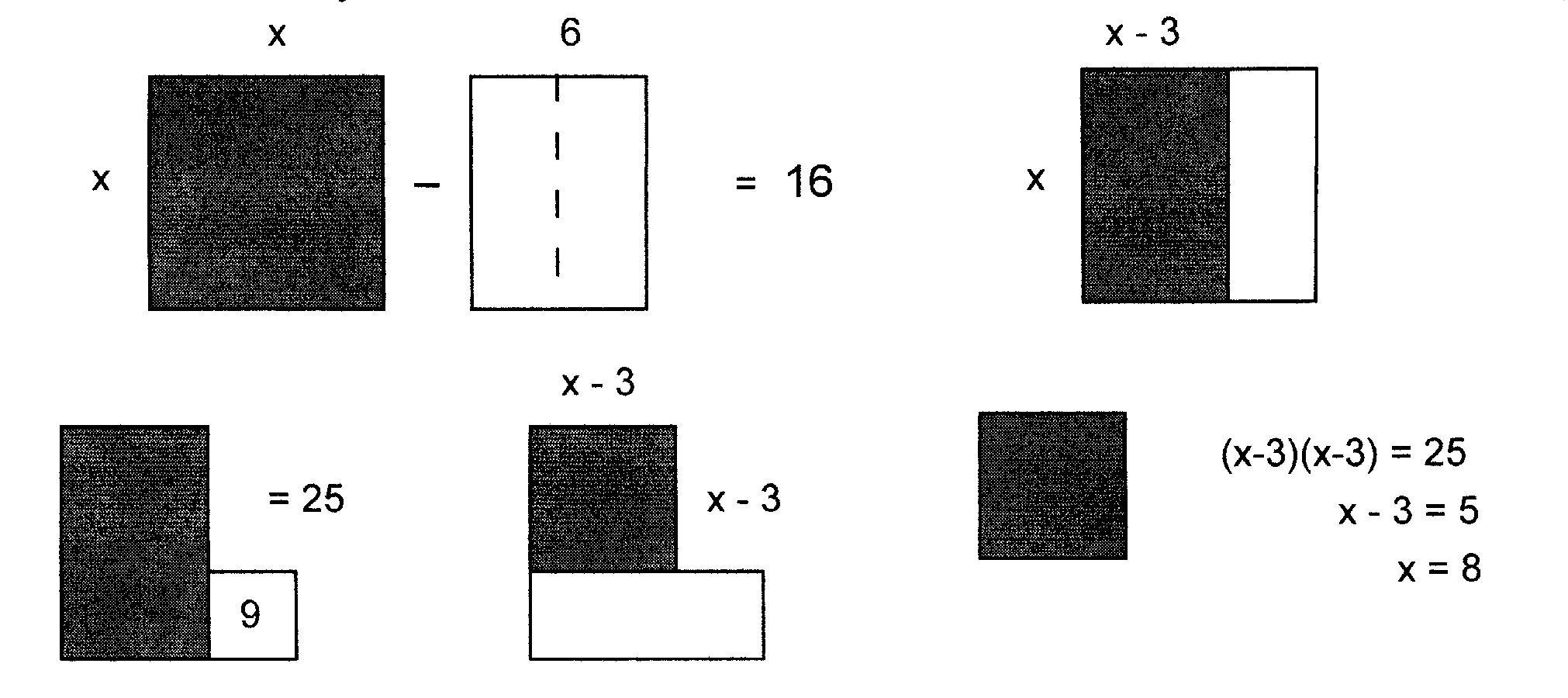
By trying to teach completing the square i have learned so much about a topic that i thought i understood as a teenager. B 22 1 22 b 2 2 1 2 2. The area of the square is equal to xb2 2 square units. Solve by completing the square x24x8.
X b 2 b 2 c. Frac 3 23 2 on the lhs to form a perfect square x2 3x frac. Step 6subtract 3 from each side. How to complete the square with a coefficient step 1.
The square is finally complete. Add a to both sides remember the plusminus sign. Now you are done completing the square and it is time to solve the problem. Divide the middle term by 2 then square it like in the first set of practice problems.
The completing the square method means that we transform a quadratic equation in the usual form of x 2 2bx c and put it in this format. Wwwmathcentreacuk 2 c mathcentre 2009. X2 6 x 9 2 9. The most common use of completing the square is solving quadratic equations.
Move all terms containing x x x and y y y to one side and the constant term if there is to the other side. Simplify the right hand side. Enter the expression in the input field step 2. To complete the square when a is greater than 1 or less than 1 but not equal to 0 factor out the value of a from all other terms.
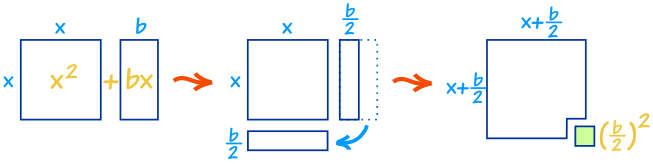
To create a trinomialsquareon the left side of the equation find a value that is equal to the squareof halfof bb. It would hence be correct to say that. Add 1 1 to both sides of the equation. Frac 12 2 6 62 36.
Square a and add it to the left side of the equation to complete into a perfect square. X 2 6 x 7 2 0. For example to solve the equation s2 6s 5 0 the first step is put the constant term on the opposite side of the equation as the terms that contain the variables by subtracting 5 from both sides to get s2 6s 5. The remaining area is equal to c b 2 4 square units.
Completing the square helps when quadratic functions are involved in the integrand. Introduce a new constant. Re write the left side into x a 2 form. The complete the square method rewrite the quadratic expression ax2 bxc in the form ax2 bx c by moving the constant term c to the right side of the equation.
Finally the variable value for the given expression will be displayed in the new window. Learn how to solve a quadratic equation by completing the square. In the given quadratic function y ax 2 bx c factor a from the first two terms of the quadratic expression on the right side. Y x2 8x 1 if the a doesnt equal 1 factor it out of the brackets and place it in front.
With straightforward steps and fill in the blank methods we will solve various polynomial equations using the method of completing the square. We write the polynomialequation into standard form with leading coefficient equal 1 divide all coefficients by. To complete the square means to create a polynomial with three terms trinomial that is a perfect square. A magic square is an arrangement of numbers in a square in such a way that the sum of each row column and diagonal is one constant number the so called magic constant this article will tell.
The left hand side is now the perfect square of x 3. Now that you have a proper quadratic terma x 2 b x cax2 bx c ax2 bxc you need to factor outaa a. Standard form to vertex form by completing the square steps step 1. Step 5use the square root property and take the square root of each side dont forget the plus or minus.
First subtract from both sides. Now complete the square the same way we did above. 2 2 x 2 12 2 x 7 2 0 2. Thus displaystyle left frac54 right2 is added to both sides of the equation.
To solve x 2 bx c 0 by completing the square we first move the constant c to the right side x 2 bx c. Now we will need to look at the term that is. Derive r from the ratio first two coefficients. Add the same number to the right side of the equation.
Here is my lesson on deriving the quadratic formula. In the given quadratic equation ax 2 bx c 0 divide the complete equation by a coefficient of x 2. Strategies for completing the square ellipses. Completing the square is a technique for manipulating a quadratic into a perfect square plus a constant.
Substitute into equation and distribute. Take the square root of both sides. In this case add the square of half of 6.

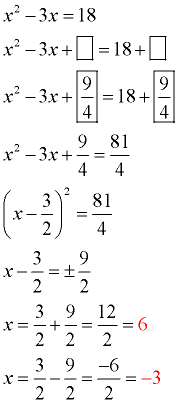



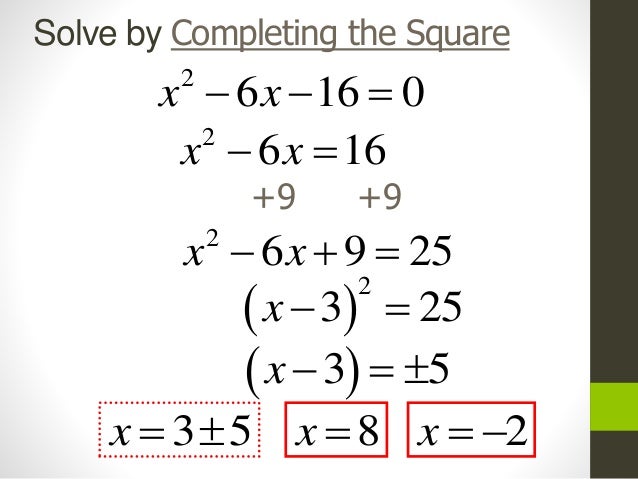
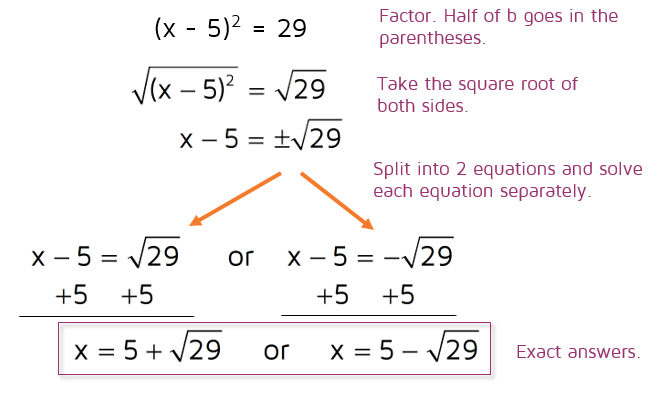




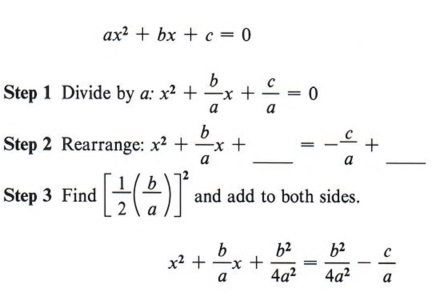
















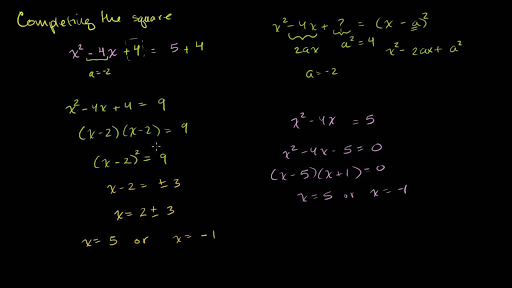



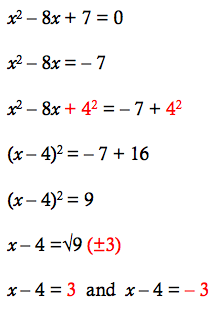
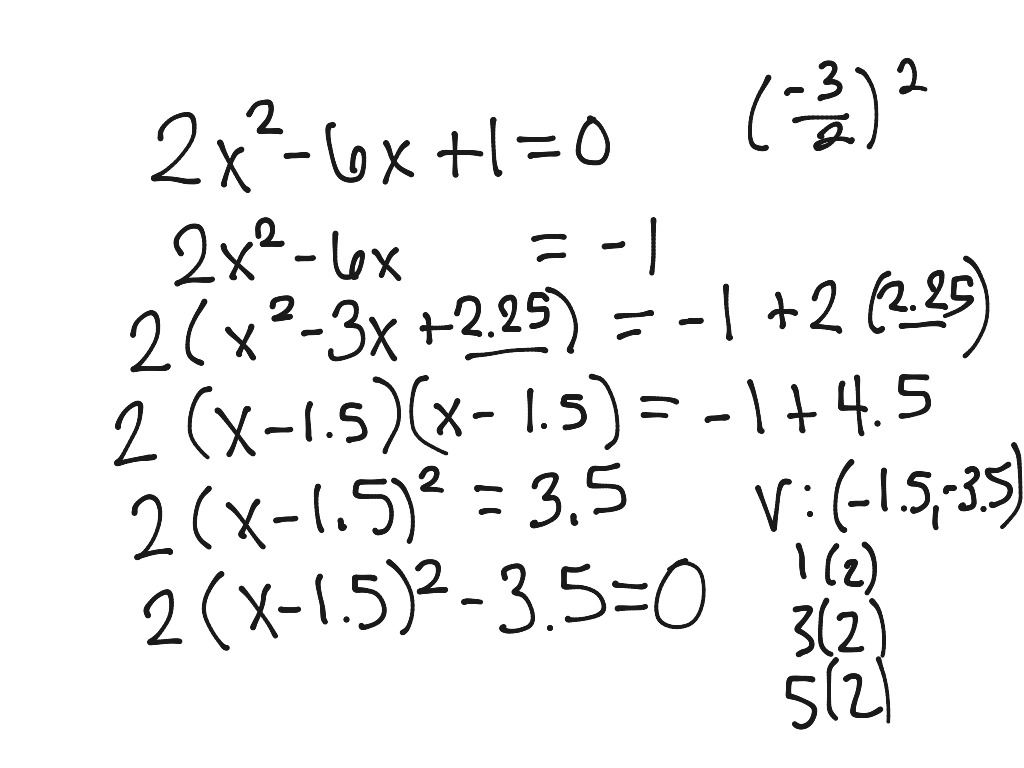




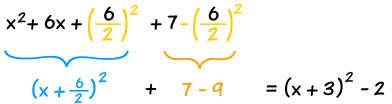
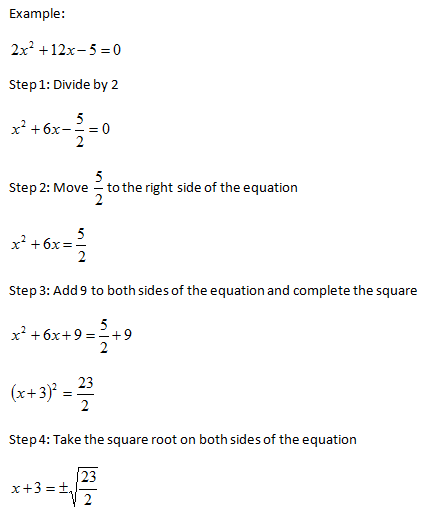


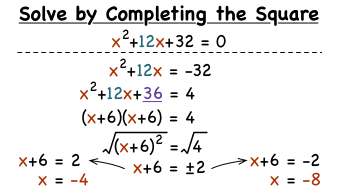
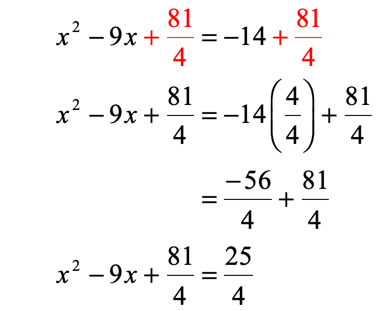

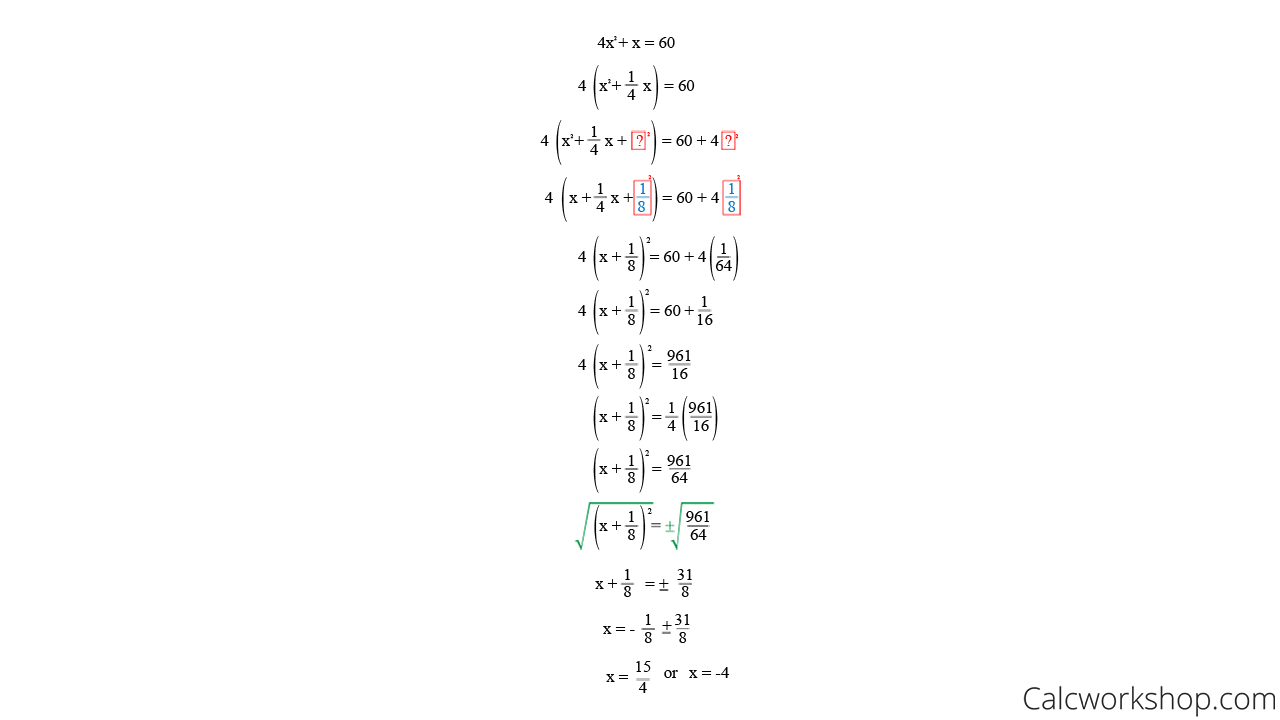


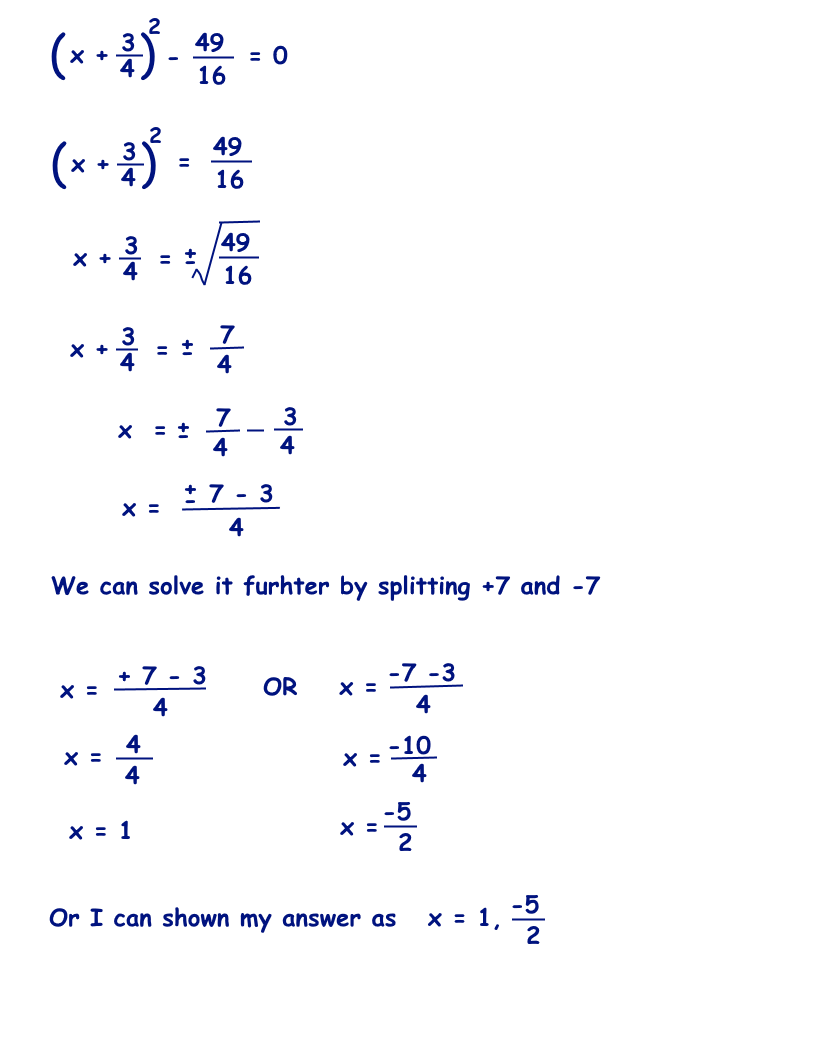



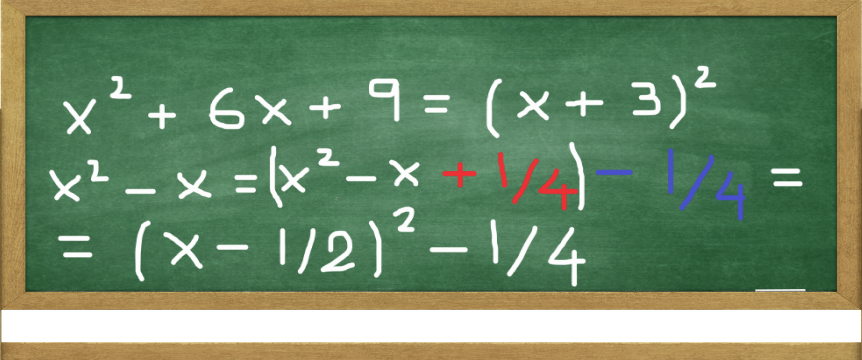
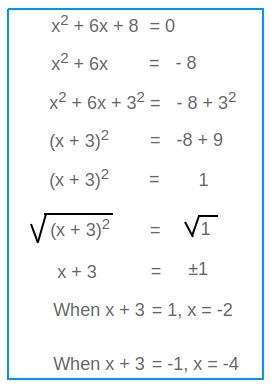

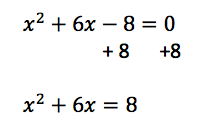

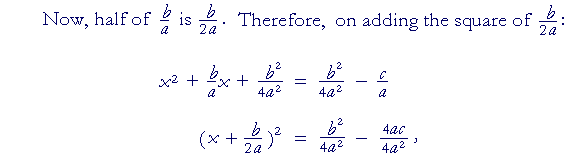
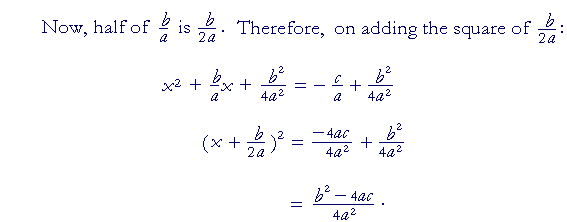





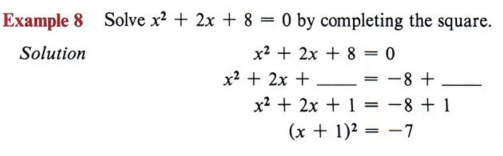




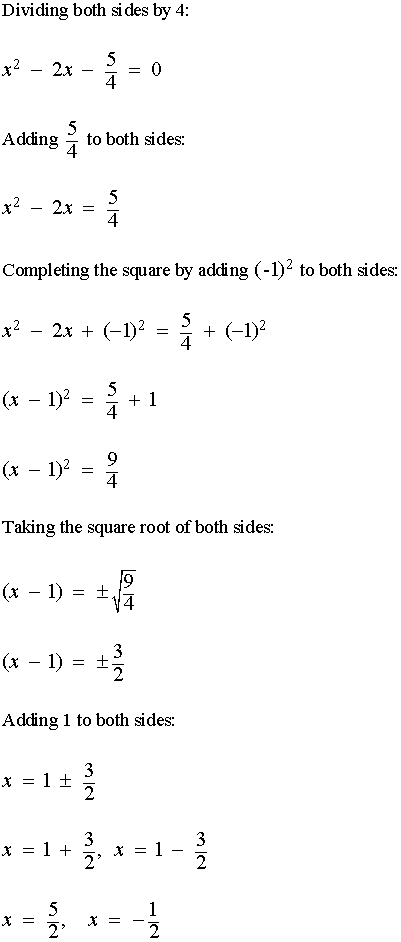



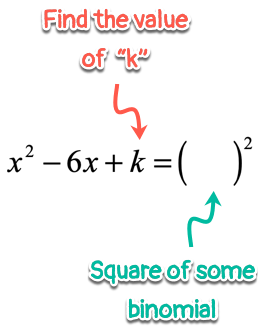






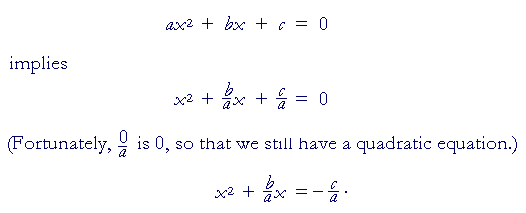
/SolveQuad1-56a602865f9b58b7d0df73fc.jpg)