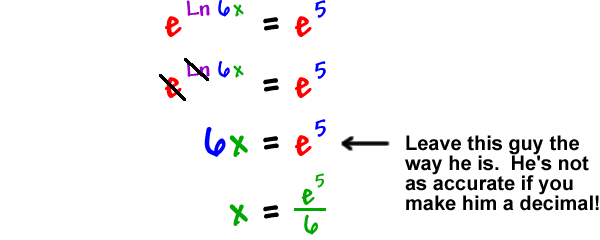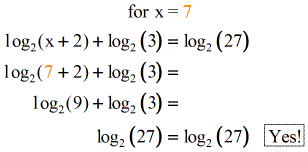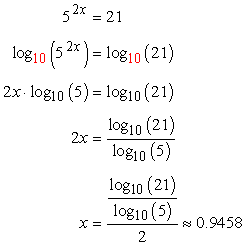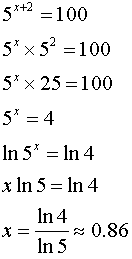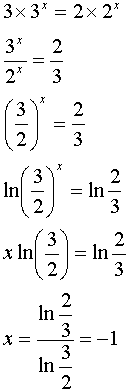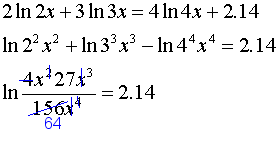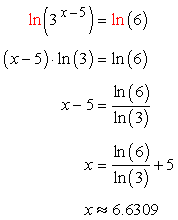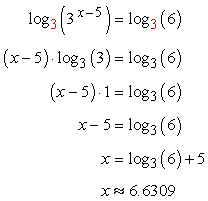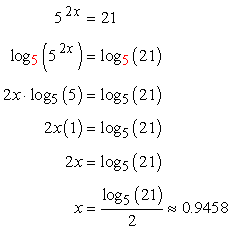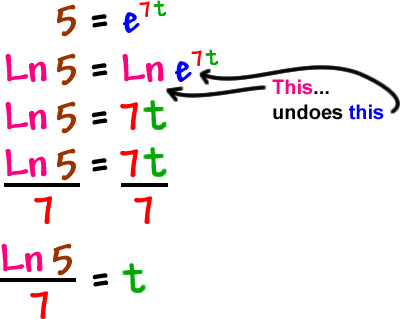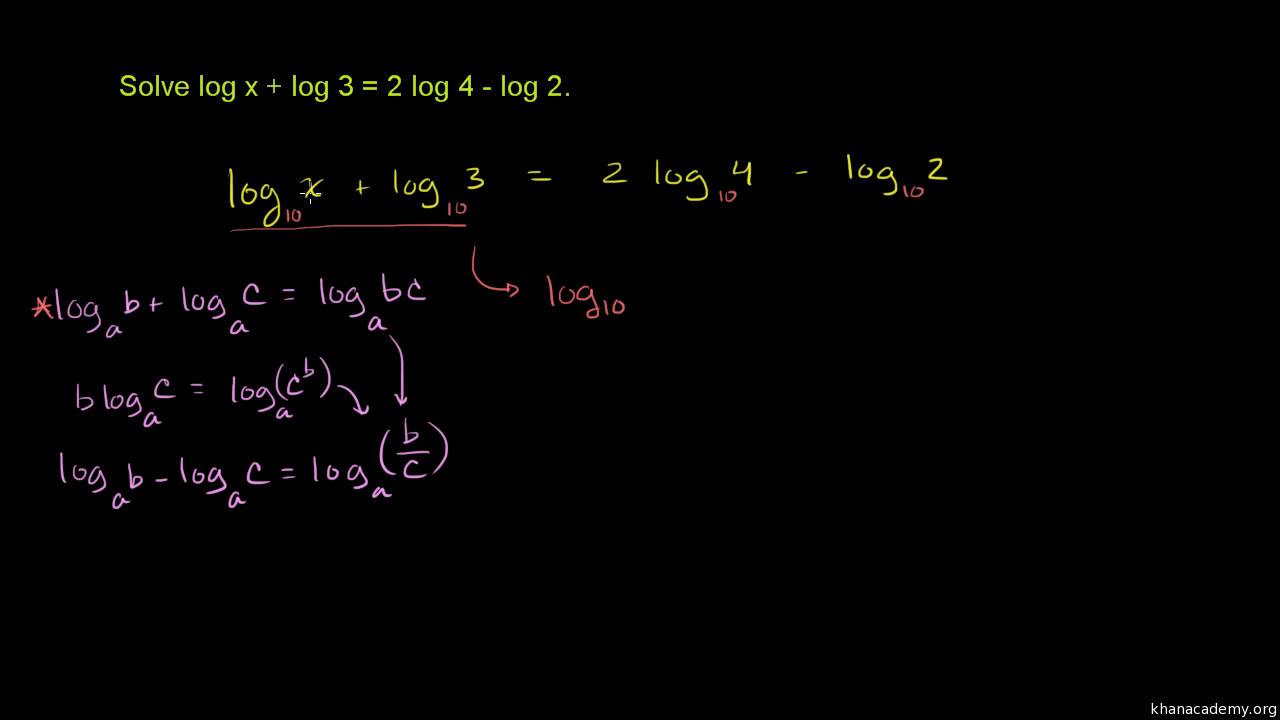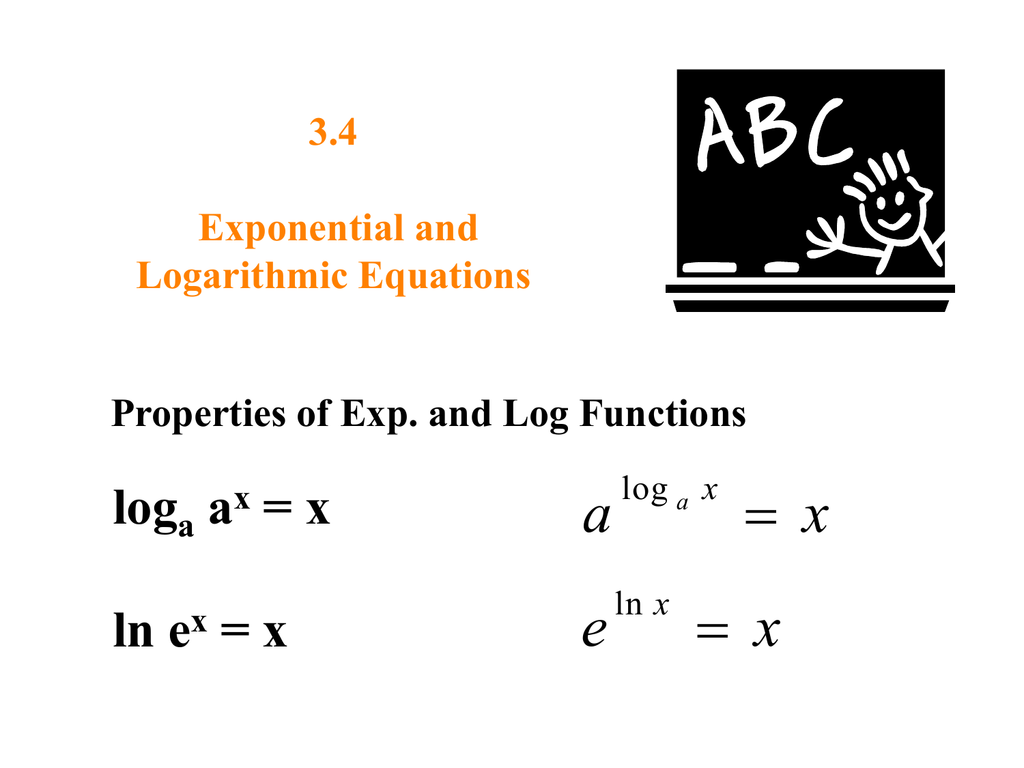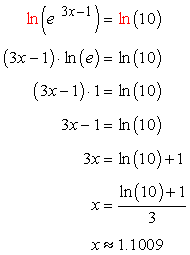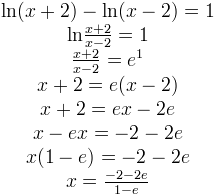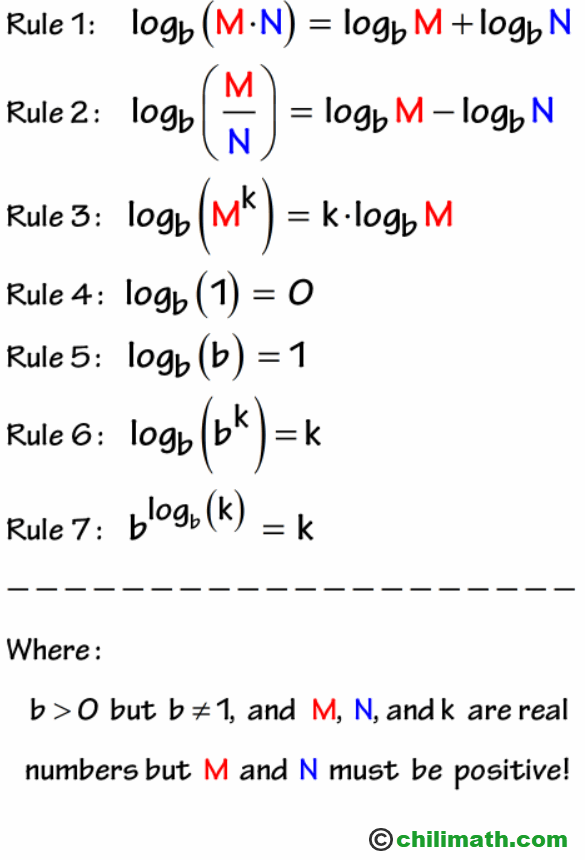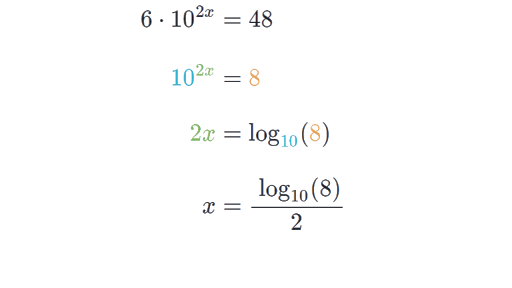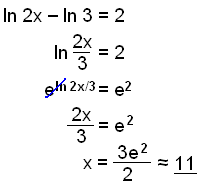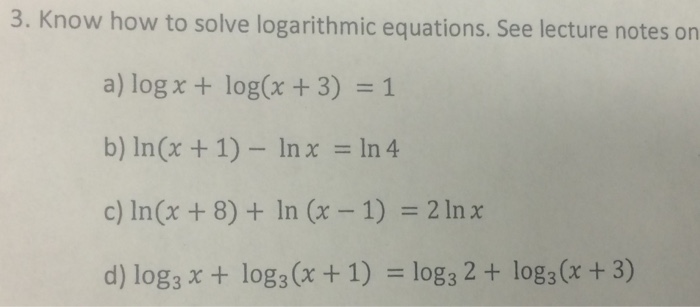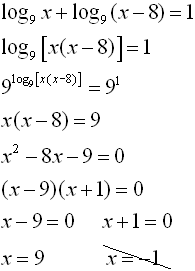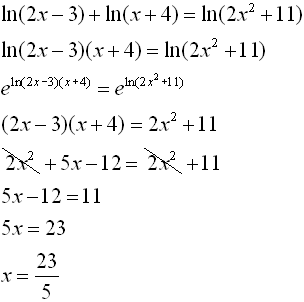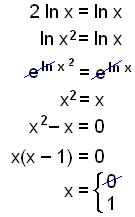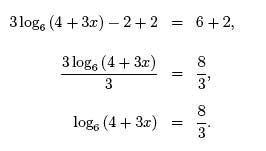How To Solve Logarithmic Equations With Ln

Finally to solve ln x ln x 5 ln 36 we first condense the natural logs on the left side of the equation to get ln xx 5 ln 36 then match up the numbers inside the natural logs to get xx 5 36 and solve from there. Step 1let both sides be exponents of the base e. On the left hand side the e and ln cancel leaving just 3x.
how to solve logarithmic equations with ln

Namely the natural log or the common log.

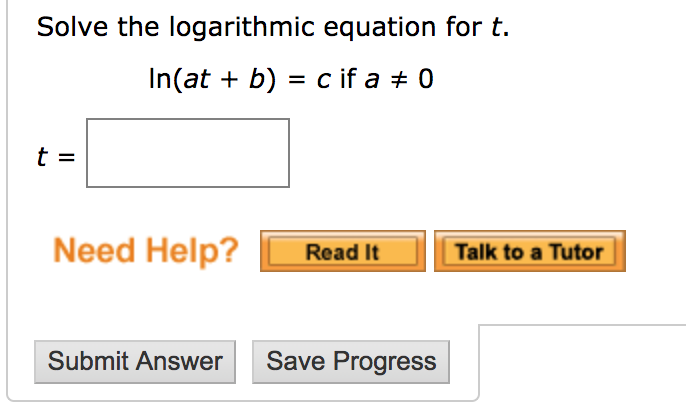
How to solve logarithmic equations with ln. On the left hand side the 10 and log cancel leaving just 2x. In order to solve this type of equations we must leave only one logarithm in each member of the equation. Solve the logarithmic equation ln x 6 log x 6 4. We can check this answer by substituting it back in for x.

A logarithmic equation is an equation which involves at least one unknown variable where a logarithmic expression appears in at least one side of the equation. X log 2 30 ln 3 0 ln 2 small dfrac ln 30 ln 2 ln2ln30. The logarithm is already by itself. In this type the variable you need to solve for is inside the log with one log on one side of the equation and a constant.

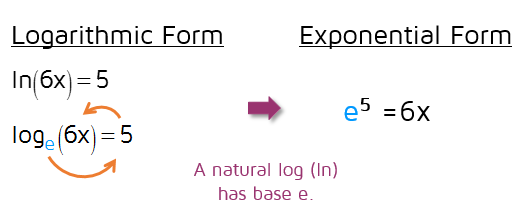
To solve a logarithmic equation rewrite the equation in exponential form and solve for the variable. Get ready to write the logarithmic equation into its exponential form. That conversion looks like this. Once we have only one logarithm on both sides of the equation we can eliminate the logarithms and thus be able to clear the unknowns.

The base of the log is 10 so we must raise both sides of the equation to be powers of 10. First wed need to apply the change of base formula to convert the expression into something in a base that our calculators can understand. An example of a logarithmic equation is ln x 2ln x ln 3 lnx 2lnxln3. Solution to example 6 use the change of base formula to rewrite log x 6 as.

Use the quotient rule to condense the log expressions on the left side. In addition each logarithm cannot be multiplied by any number. Logarithmic equations take different forms. Move all the logarithmic expressions to the left of the equation and the constant to the right.

As a result before solving equations that contain logs you need to be familiar with the following four types of log equations. The equation lnx8 can be rewritten. Step 1isolate the logarithmic term before you convert the.