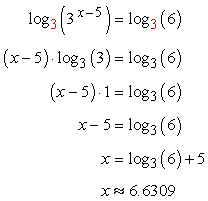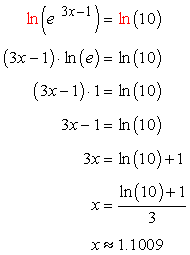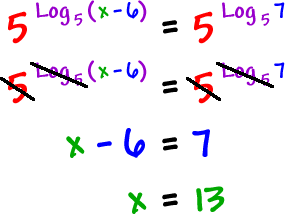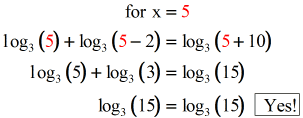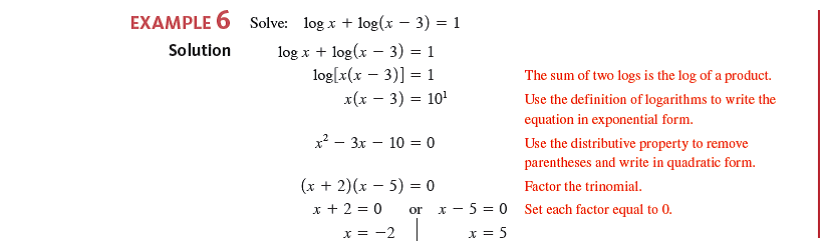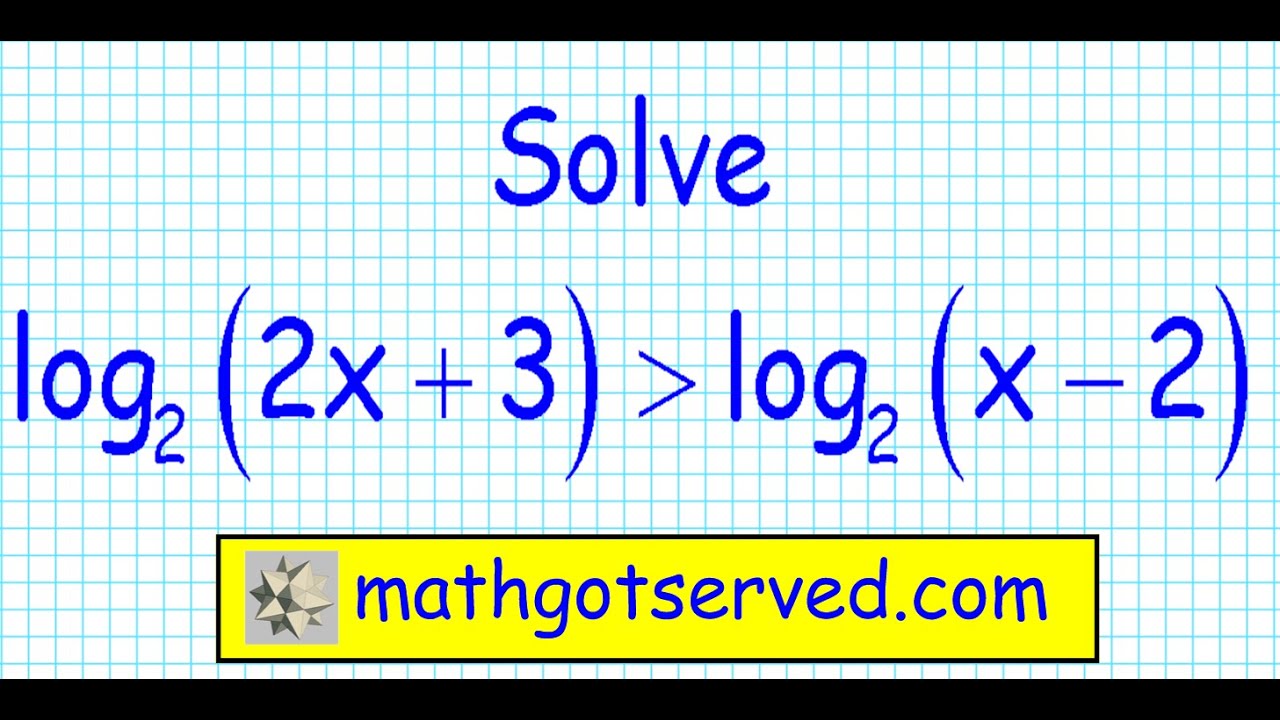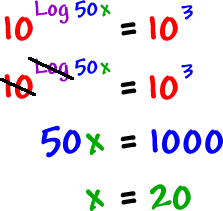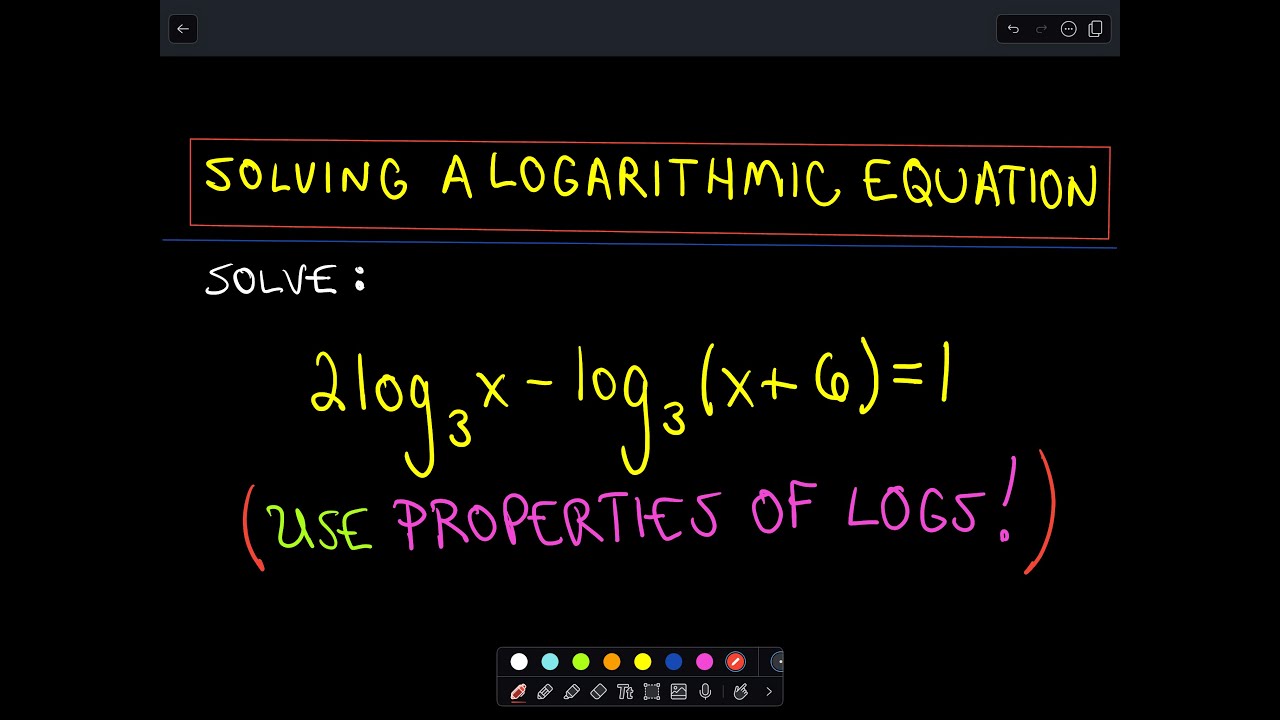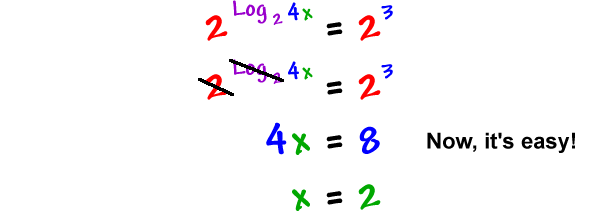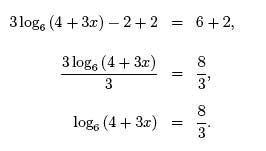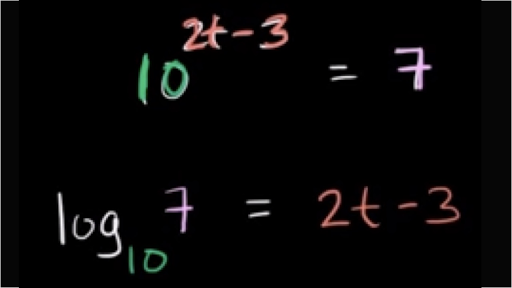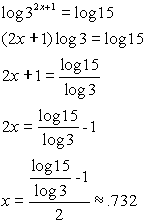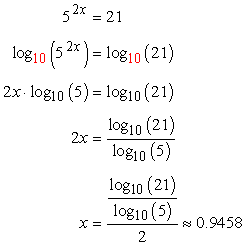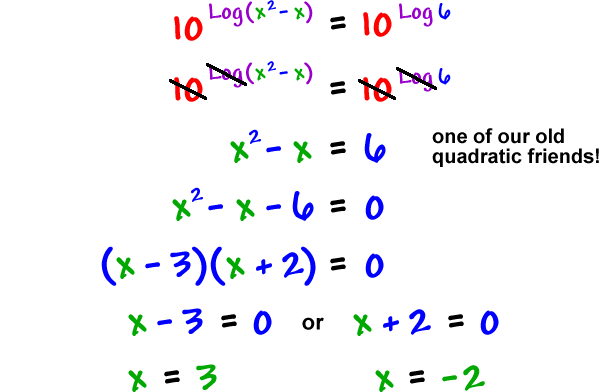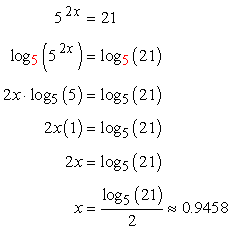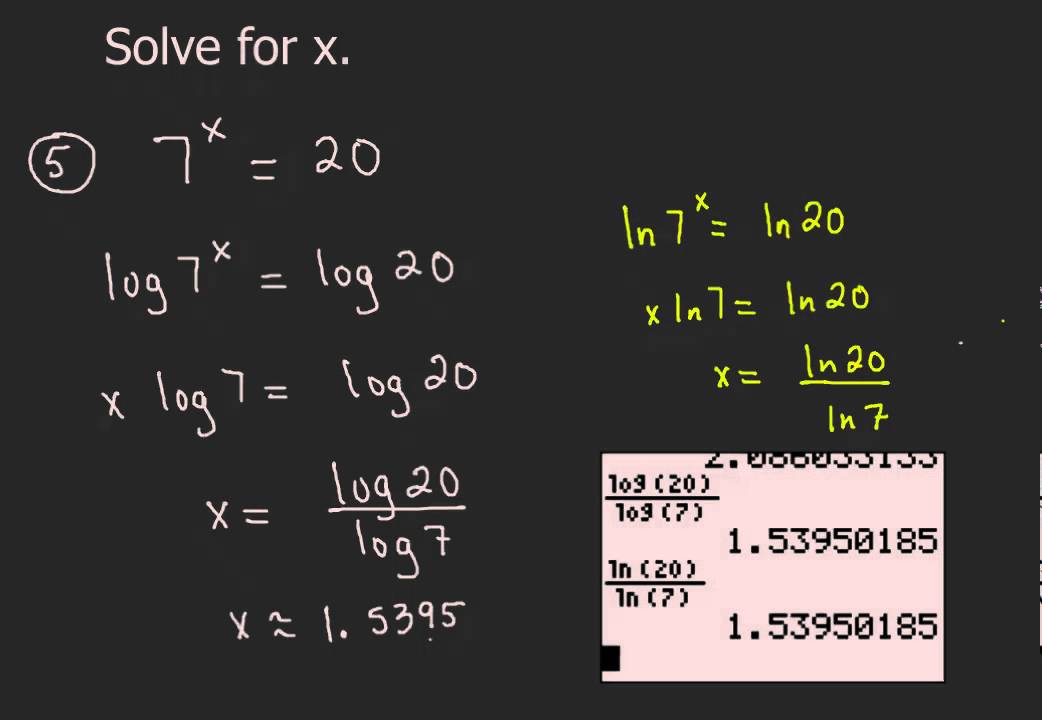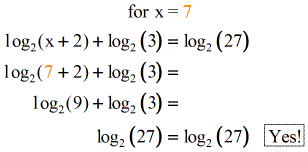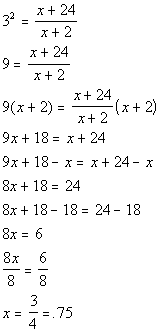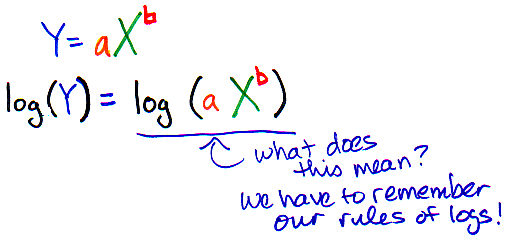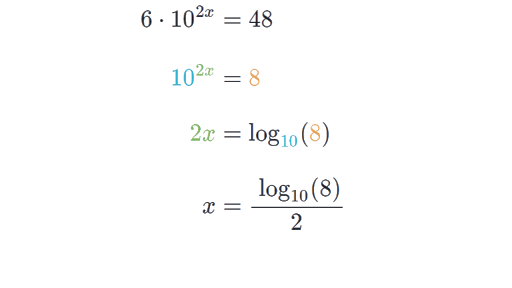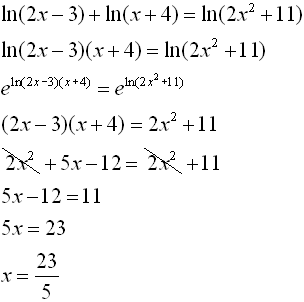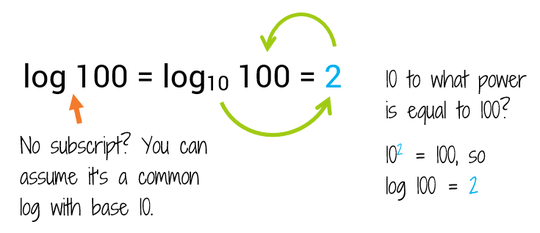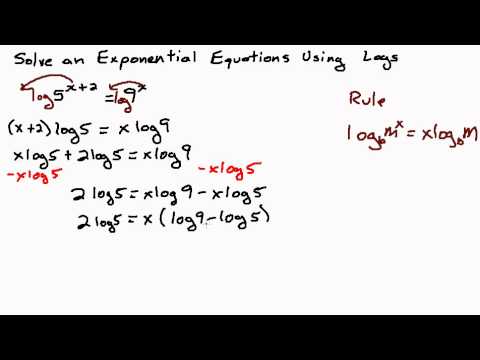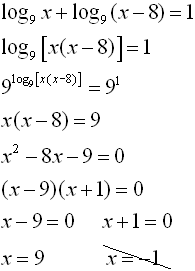How To Solve Log Equations With Logs On Both Sides

When i take the log of both sides of an equation i can use any log i like base 10 log base 2 log natural log etc but some are sometimes more useful than others.

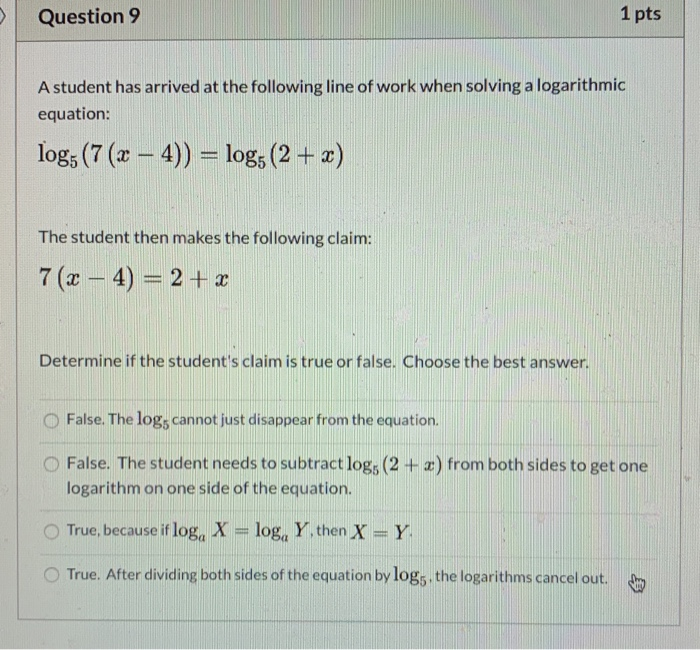
How to solve log equations with logs on both sides. Evaluating logarithms using change of base formula. The equations with logarithms on both sides of the equal to sign take the form of log m log n which is the same as m n. You can drop the log base 3 from both sides to get. Take the log of both sides.

Using the common log on both sides gives you log 4 3 x 1 log 11. You can take any log you want but remember that you actually need to solve the equation with this log so you should with common or natural logs only. Product rule of logarithms. If you have the same operation on both sides of an equation they cancel each other out.

Use the power rule to drop down the exponent. You could simplify both sides first to get 2x 12. Keep in mind that this only works when the logarithms on both sides of the equation have the same base. This step gives you 3x 1log 4 log 11.

If you had a logarithm with base 3 on one side and a logarithm with base 7 on the other side they wont cancel out. You can then divide both sides by 2 to get the x all by itself. You can combine all the logs so that you have one log on the left and one log on the right and then you can drop the log from both sides. Converting from exponential form to logarithmic form.

Log 2 2 x log 2 30 any log of the logs base returns a value of 1 so log22 1. If the logarithms have are a common base simplify the problem and then rewrite it without logarithms. Solving exponential equations with logarithms. Here i used different colors to show that since we have the same base if not explicitly shown it is assumed to be base.

Simplify the exponent still referring to the leftmost term then condense the logs on both sides of the equation. Combining product rule and quotient rule in logarithms. Which you can solve easily by using algebra techniques. For example to solve log 3 x 1 log 3 x 4 log 3 5 first apply the quotient rule to get.

Use the quotient rule on the left and product rule on the right.