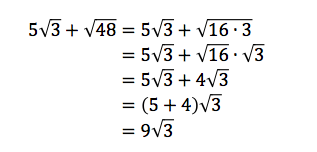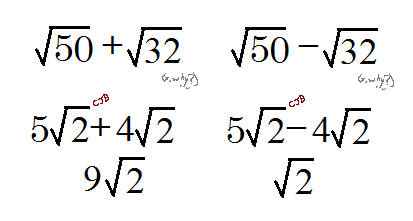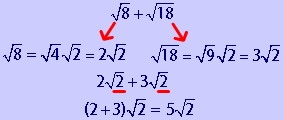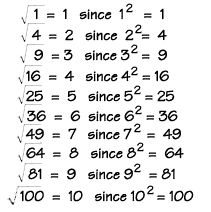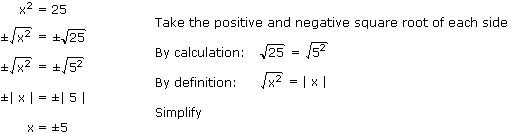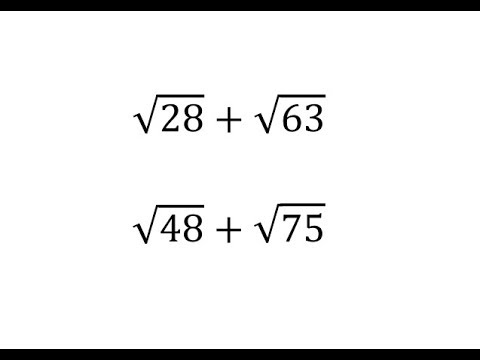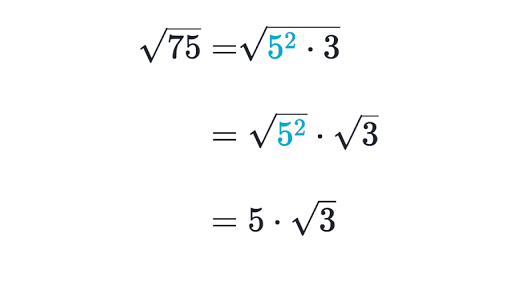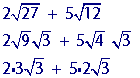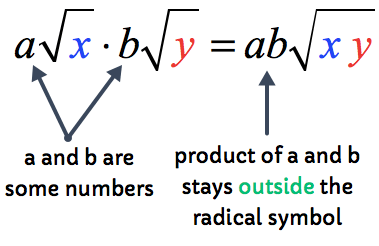How To Add Two Square Roots

You can only add square roots or radicals that have the same radicand.

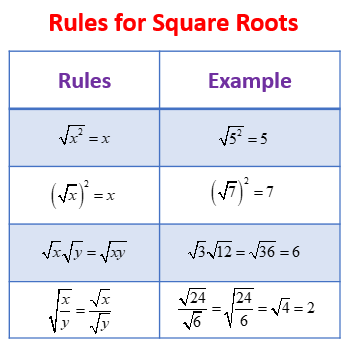
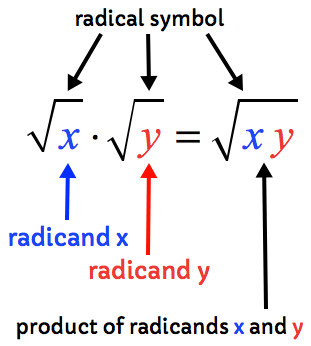
How to add two square roots. Squaring a square root causes one of the square roots to disappear leaving the expression that was inside of the square root. Just as you cant add apples and oranges so also you cannot combine unlike radical terms. Larger sequences of square roots can be added the same way. Combining square roots square roots which use the radical symbol are nonbinary operations operations which involve just one number that ask you what number times itself gives you this number under the radical.

You can subtract square roots with the same radicand which is the first and last terms. But you might not be able to simplify the addition all the way down to one number. Only add the. This radical expression is already simplified so you are done.

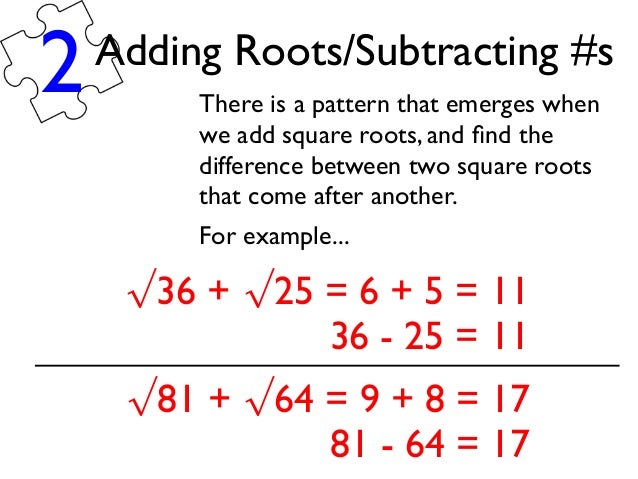
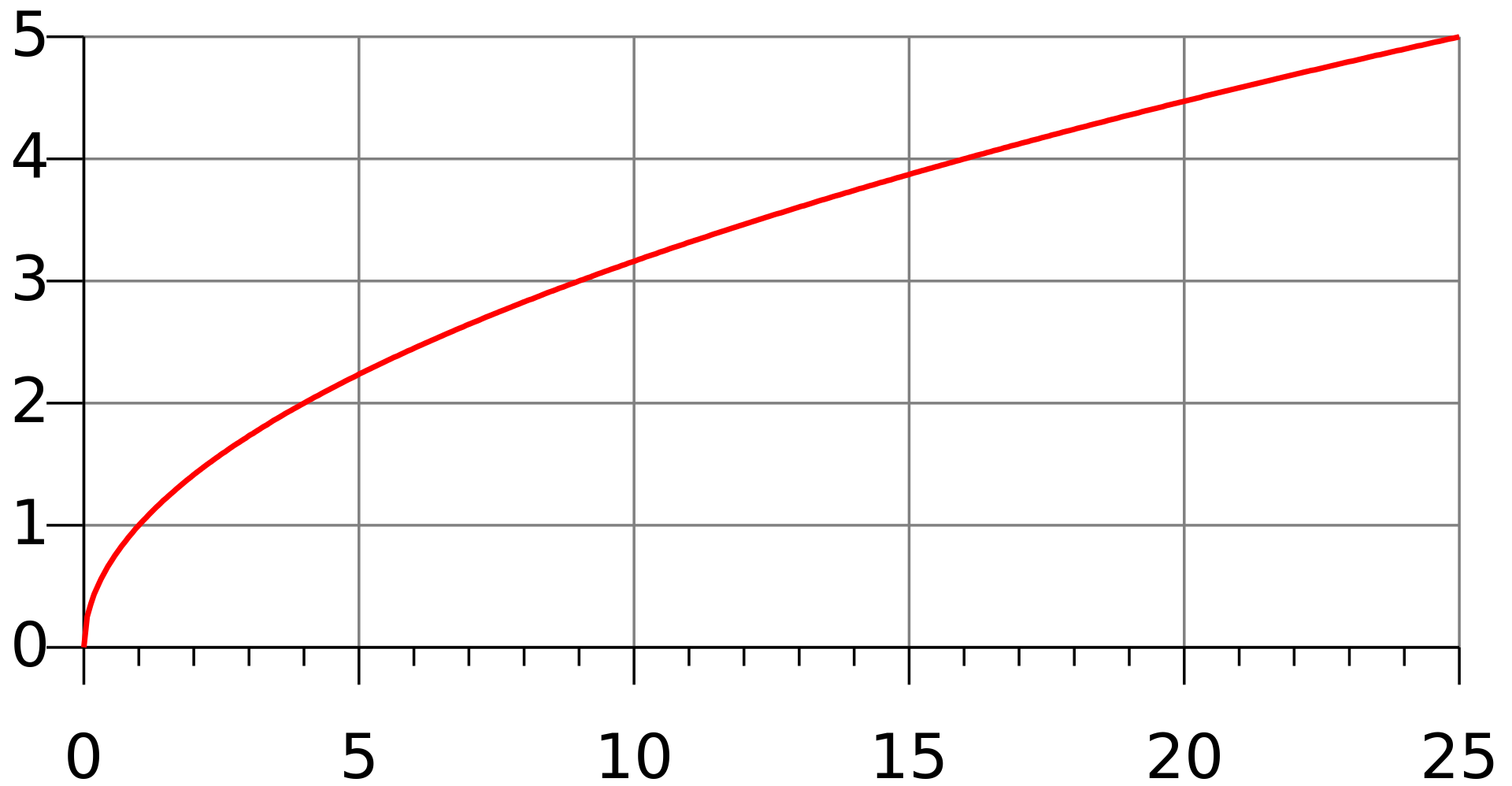
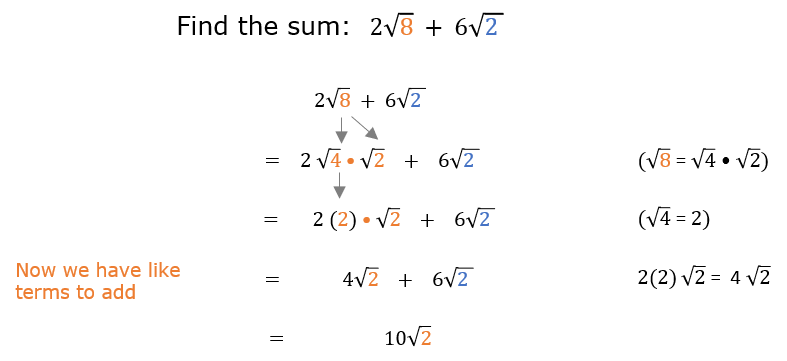
For instance its fine to add together 4 square root of 2 and 5 square root of 2 since the square roots are the same. If you want to add 2 about 1414 to 3 about 1732 youd get about 3146 which is approximately the sum of the two square roots. This would give you 9 square root of 2 since 4 5 9. In order to be able to combine radical terms together those terms have to have the same radical part.

Adding square roots 1. Place a 1 in front of any square root that doesnt already have a coefficient. Square each side of the equation. To add and subtract square roots you need to combine square roots with the same radical term.

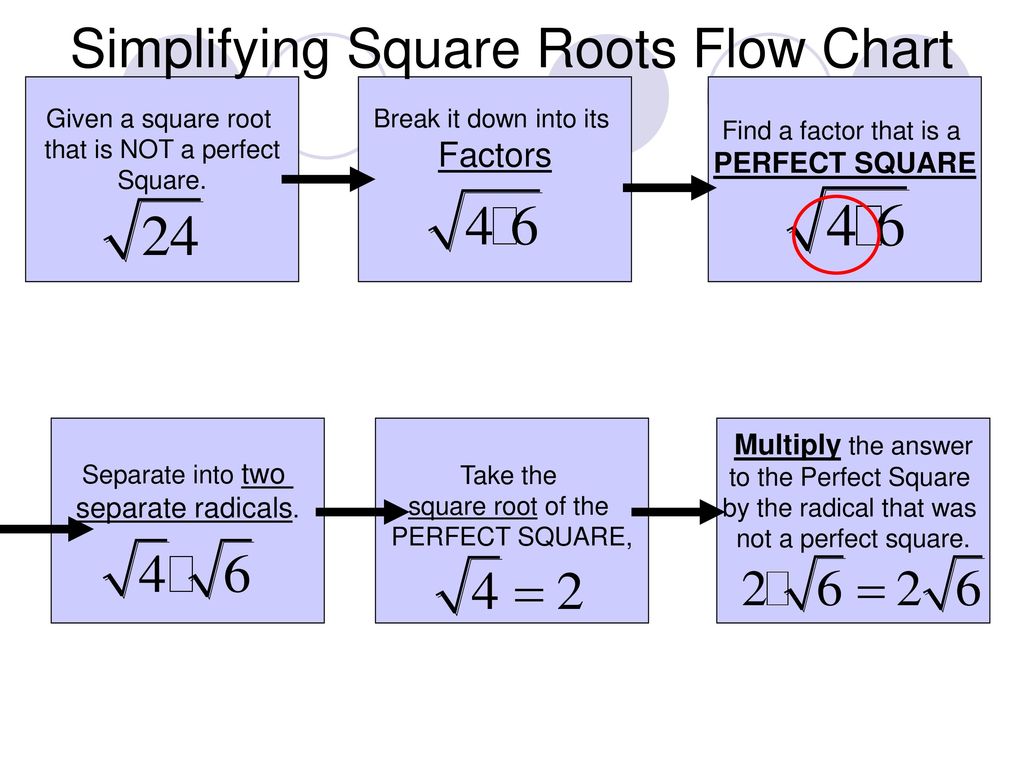
This means that you add or subtract 23 and 43 but not 23 and 25. There are many cases where you can actually simplify the number inside the radical to be able to combine like terms and to freely add and subtract square roots. Check to see if you can simplify either of the square roots. If you can then simplify.

Just as you can only add together terms with like variables such as 3x and 4x you can only add terms with imperfect square roots if they have the same square roots. Just as with regular numbers square roots can be added together. Consider the following example. The only difference is that both square roots in this problem can be simplified.

The 1 is always understood and so is. Check for square roots with the same radicand. The same rule goes for subtracting.